Bài toán chọn tất- Bài toán nâng bậc Xác suất nâng cao -Luyện thi ĐGNL Bộ công an 2025
Bài toán Von Koch- bông tuyết Vôn Kốc -Luyện thi HSG giỏi 9 10 điểm
Bài toán chọn tất- Bài toán nâng bậc Xác suất nâng cao -Luyện thi ĐGNL Bộ công an 2025
Bài toán người tuyết - tính thể tích người tuyết
Bài toán chọn tất
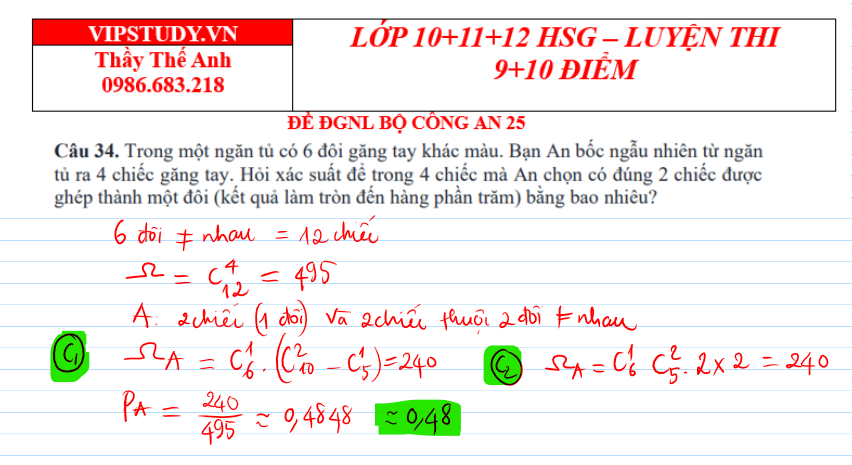
Có 6 đôi găng tay (tức 12 chiếc, mỗi đôi gồm 2 chiếc giống nhau). Rút ngẫu nhiên 4 chiếc. Tính xác suất để đúng 2 chiếc trong 4 chiếc ghép thành một đôi (tức có đúng 1 đôi hoàn chỉnh và 2 chiếc còn lại không khớp với nhau).
Bài toán nâng bậc
Trong kỳ thi nâng bậc, một công nhân phải chọn ngẫu nhiên (bốc thăm) một trong hai loại sản phẩm A hoặc B trong một thùng phiếu có 4 phiếu sản phẩm loại A, 6 phiếu sản phẩm loại B. Sau đó, người công nhân phải gia công 2 sản phẩm của loại vừa bốc được. Để đỗ trong kỳ thi này thì cả 2 sản phẩm gia công đều phải đạt tiêu chuẩn.
Xác suất để công nhân đó gia công được sản phẩm loại A đạt tiêu chuẩn là 0,8 và xác suất để gia công được sản phẩm loại B đạt tiêu chuẩn là 0,9. Sau khi thi xong, người công nhân đó bị trượt. Hỏi xác suất để người đó chọn vào đúng sản phẩm loại A là bao nhiêu?

BÀI TƯƠNG TỰ LUYỆN THI BỘ CÔNG AN
Bài 1.
Một hộp có 5 phiếu màu đỏ (ứng với loại sản phẩm X) và 7 phiếu màu xanh (ứng với loại sản phẩm Y). Một công nhân rút ngẫu nhiên 1 phiếu rồi gia công 3 sản phẩm loại đó.
-
Xác suất để mỗi sản phẩm loại X đạt chuẩn là 0,7.
-
Xác suất để mỗi sản phẩm loại Y đạt chuẩn là 0,9.
Công nhân bị trượt vì trong 3 sản phẩm có ít nhất 1 cái không đạt. Tính xác suất người đó đã chọn phiếu màu đỏ.
Bài 2.
Trong kỳ thi nghề, thí sinh chọn ngẫu nhiên 1 trong 2 loại đề: Đề A (chiếm 3/8 số phiếu) hoặc Đề B (chiếm 5/8 số phiếu). Sau đó làm 2 bài thực hành.
-
Với đề A, xác suất làm đúng 1 bài là 0,85.
-
Với đề B, xác suất làm đúng 1 bài là 0,9.
Để qua vòng thi, thí sinh phải làm đúng cả 2 bài. Kết quả: thí sinh trượt. Hỏi xác suất thí sinh đó đã chọn đề A.
Bài 3.
Một công ty có 2 loại máy:
-
Máy loại I: chiếm 40%, xác suất để sản phẩm đạt chuẩn là 0,95.
-
Máy loại II: chiếm 60%, xác suất để sản phẩm đạt chuẩn là 0,8.
Một công nhân chọn ngẫu nhiên một máy, sản xuất 2 sản phẩm. Kết quả: ít nhất 1 sản phẩm không đạt chuẩn. Hỏi xác suất công nhân đã chọn máy loại II.
Bài 4.
Có 2 lớp học:
-
Lớp A có 30% học sinh, mỗi học sinh có xác suất làm đúng một bài toán là 0,9.
-
Lớp B có 70% học sinh, xác suất làm đúng bài toán là 0,7.
Chọn ngẫu nhiên 1 học sinh và cho làm 2 bài toán. Học sinh này bị sai ít nhất 1 bài. Hỏi xác suất học sinh đó thuộc lớp B.
Bài 5.
Một xưởng có 3/10 số công nhân quen làm sản phẩm loại M, còn lại 7/10 quen làm loại N.
-
Nếu làm loại M: xác suất để một sản phẩm đạt chuẩn là 0,85.
-
Nếu làm loại N: xác suất đạt chuẩn là 0,95.
Một công nhân được chọn ngẫu nhiên, gia công 2 sản phẩm theo loại mình quen. Kết quả: công nhân bị trượt vì cả 2 sản phẩm không đều đạt chuẩn. Hỏi xác suất công nhân đó thuộc nhóm làm loại M.





