Bài toán Von Koch- bông tuyết Vôn Kốc -Luyện thi HSG giỏi 9 10 điểm
Bài toán Von Koch- bông tuyết Vôn Kốc -Luyện thi HSG giỏi 9 10 điểm
Bài toán chọn tất- Bài toán nâng bậc Xác suất nâng cao -Luyện thi ĐGNL Bộ công an 2025
Bài toán người tuyết - tính thể tích người tuyết
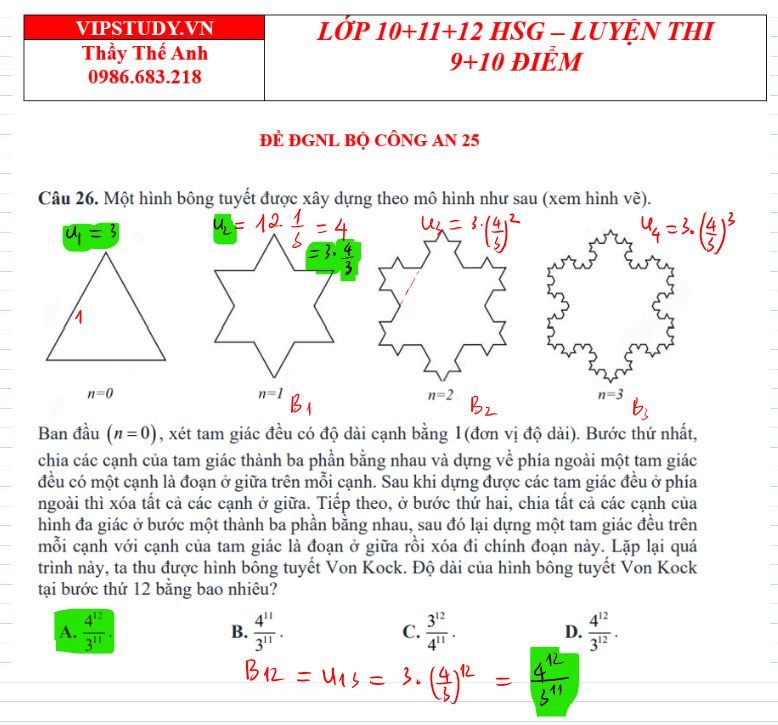
Bông tuyết Vôn Kốc (von Koch)
Bông tuyết Vôn Kốc (được đặt theo tên nhà toán học Thụy Điển, Niels Fabian Helge von Koch, 25 tháng 1 năm 1870 – 11 tháng 3 năm 1924) được xây dựng bằng phương pháp lặp như sau: Cho một tam giác đều. Ở bước một, chia mỗi cạnh của tam giác thành ba đoạn bằng nhau, dựng tam giác đều trên đoạn ở giữa (ở bên ngoài tam giác đã cho) rồi xóa cạnh đáy của tam giác đều này thì được một đường gấp khúc kín. Ở mỗi bước tiếp theo, chia mỗi đoạn của đường gấp khúc kín thành ba đoạn con bằng nhau, dựng tam giác đều trên đoạn con ở giữa (ở bên ngoài đường gấp khúc kín đó) rồi xóa cạnh đáy. Cứ làm thế mãi thì được “bông tuyết Vôn Kốc”.
Một hình bông tuyết được xây dựng theo mô hình sau: Ban đầu , xét tam giác đều có độ dài cạnh bằng 1 (đơn vị độ dài). Bước thứ nhất, chia các cạnh của tam giác thành ba phần bằng nhau và dựng về phía ngoài một tam giác đều có một cạnh là đoạn ở giữa trên mỗi cạnh. Sau khi dựng được các tam giác đều ở phía ngoài thì xóa tất cả các cạnh ở giữa. Bước thứ hai, chia tất cả các cạnh của hình đa giác ở bước một thành ba phần bằng nhau, sau đó lại dựng một tam giác đều trên mỗi cạnh với cạnh của tam giác là đoạn ở giữa vừa xóa đi chính đoạn này. Lặp lại quá trình này, ta thu được hình bông tuyết Von Koch. Độ dài của hình bông tuyết Von Koch tại bước thứ 12 bằng bao nhiêu?
BÀI TOÁN TƯƠNG TỰ





